طريقة غوص

طريقة غوص

هي من بين أشهر الخوارزميات لحل نظمات المعادلات الخطية.

---

لمحة تاريخية

طريقة غوص هي خوارزمية مخصصة لحل نظمات المعادلات الخطية وإيجاد درجة مصفوفتها وحساب معكوس المصفوفة. يتم تطبيق عمليات الصف الأساسية لتخفيض المصفوفة على صورة مصفوفة مثلثية. يرجع اكتشاف جزء من هذه الخوارزمية إلى حوالي 150 قبل الميلاد في الصين، وقد تم إيضاحها في الفصل الثامن للمصفوفات المربعة في الكتاب الصيني المسمى "الفصول التسعة في فن الرياضيات" (九章算术). وقد تم الإشارة إليها من من طرف أحد علماء الرياضيات الصينين في حقبة الممالك الثلاث ويدعى "ليو خوي" (刘徽). العربية: طريقة غوص الإنجليزية: Gauss Method الفرنسية: Methode de Gauss

---

المبدأ

• يساعد الخوارزم على الحصول على نظمة مثلثية مكافئة ولـحل لهذه النظمة.
•  ليكن:  A⁽¹⁾ = A  و b⁽¹⁾ = b.
• نفترض أن  a₁₁⁽¹⁾غير منعدم وهذا يمكن الحصول عليه بتبديل سطور الجدول.
  في الجدول (A⁽¹⁾ | b⁽¹⁾)  نقوم بتأليفة خطية لسطرين l_i و l₁  حيث  i = 2,... n  
• نعوض  l_i  بـ 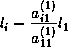    حيث i=2,...n

 نحصل إذا على المصفوفة بالشكل التالي:

  و   

النظمة الأصلية مكافئة للنظمة الجديدة  ⁽A⁽²⁾ x = b⁽². 

نعيد تأليفة خطية مشابهة لسطرين  l_i و l₂  بحيث i = 3,... n  لـ   (A⁽²⁾ | b⁽²⁾) بطريقة تنعدم فيها عناصر ما تحت القطر للعمود الثاني لـ  A⁽²⁾، وهكذا حتى تصير المصفوفة مثلثية علوية.

نحل بعد ذلك النظمة المثلثية المحصل عليها.

---

الخوارزم

المرحلة 1: التحويل المثلثي لـ A، أي تحويل النظمة إلى نظمة مكافئة ذات مصفوفة مثلثية علوية.

A⁽¹⁾ = A, b⁽¹⁾ = b

المرحلة 2: لنحل النظمة المثلثية  A⁽ⁿ⁾ x = b⁽ⁿ⁾.

---

مثال

قم بحل النظمة  Ax=b حيث:

    و     

حل يدوي ( باستعمال الكسر)

المرحلة 1: التحويل المثلثي لـ A

المرحلة 2: لنحل النظمة المثلثية A⁽⁴⁾x = b⁽⁴⁾ 

 
 

---

البرمجة

• #include <math.h>
  #include <conio.h>
  #define NMAX 5
  #define N2MAX 6
  
  int sl_gauss_aff(double a[NMAX][NMAX],double b[NMAX],int n);
  
  main()
  {
   double a[NMAX][NMAX],b[NMAX];
   int i,j,n,err;
   clrscr();
   n=4;
   printf("Méthode de Gauss\n");
   a[1][1]=8;a[1][2]=-4;a[1][3]=3;a[1][4]=7;b[1]=12;
   a[2][1]=4;a[2][2]=2;a[2][3]=-6;a[2][4]=4;b[2]=1;
   a[3][1]=-16;a[3][2]=6;a[3][3]=-2;a[3][4]=-15;b[3]=-19;
   a[4][1]=6;a[4][2]=10;a[4][3]=-15;a[4][4]=10;b[4]=1;
   printf("                          A(1)                                 b(1)\n");
   for(i=1;i<=n;i++)
   {
    for(j=1;j<=n;j++)
    printf("%12.6e  ",a[i][j]);
    printf("I  %12.6e  \n",b[i]);
   }
   err=sl_gauss_aff(a,b,n);
   if(err==1)
   {
    printf("Solution:\n");
    for(i=1;i<=n;i++)
    printf("x%d =%23.16e  \n",i,b[i]);
   }
   else printf("Erreur, matrice singulière");
  }

  ---

  نتائج البرنامج
  في كل مرحلة يظهر البرنامج على الشاشة ما يلي:
  • المصفوفة  A^(k)   
  • العنصر الثاني b^(k)
    
  • ويظهر بعد ذلك حل النظمة 

•      A(1)                                 b(1)
   8.00000e+00  -4.00000e+00   3.00000e+00   7.00000e+00  I   1.20000e+01  
   4.00000e+00   2.00000e+00  -6.00000e+00   4.00000e+00  I   1.00000e+00  
  -1.60000e+01   6.00000e+00  -2.00000e+00  -1.50000e+01  I  -1.90000e+01  
   6.00000e+00   1.00000e+01  -1.50000e+01   1.00000e+01  I   1.00000e+00  
       A(2)                                 b(2)
   8.00000e+00  -4.00000e+00   3.00000e+00   7.00000e+00  I   1.20000e+01  
   0.00000e+00   4.00000e+00  -7.50000e+00   5.00000e-01  I  -5.00000e+00  
   0.00000e+00  -2.00000e+00   4.00000e+00  -1.00000e+00  I   5.00000e+00  
   0.00000e+00   1.30000e+01  -1.72500e+01   4.75000e+00  I  -8.00000e+00  
       A(3)                                 b(3)
   8.00000e+00  -4.00000e+00   3.00000e+00   7.00000e+00  I   1.20000e+01  
   0.00000e+00   4.00000e+00  -7.50000e+00   5.00000e-01  I  -5.00000e+00  
   0.00000e+00   0.00000e+00   2.50000e-01  -7.50000e-01  I   2.50000e+00  
   0.00000e+00   0.00000e+00   7.12500e+00   3.12500e+00  I   8.25000e+00  
       A(4)                                 b(4)
   8.00000e+00  -4.00000e+00   3.00000e+00   7.00000e+00  I   1.20000e+01  
   0.00000e+00   4.00000e+00  -7.50000e+00   5.00000e-01  I  -5.00000e+00  
   0.00000e+00   0.00000e+00   2.50000e-01  -7.50000e-01  I   2.50000e+00  
   0.00000e+00   0.00000e+00   0.00000e+00   2.45000e+01  I  -6.30000e+01  
  Solution:
  x1 =  4.571428571428571e+00  
  x2 =  3.357142857142856e+00  
  x3 =  2.285714285714285e+00  
  x4 = -2.571428571428572e+00  
  

ملاحظة

الشفرة تستعمل الدالة sl_gauss_aff.

تطبيقيا: من المستحسن استعمال الدالة sl_gauss_pivmax التي:

• لا تقوم بعمليات زائدة (حسا ب الصفر).
• لا تظهر كل مراحل المصفوفة الوسيطية.
• تبحث كل مرة على de pivot maximum dans la colonne pivot

  ---

  برمجة الدالة الرئيسية sl_gauss_aff
• معايير الدالة

a : المصفوفةb : العنصر الثانيn : درجة المصفوفة

القيمة الرجعية

ترجع القيمة 1 عندما تكون المصفوفة مقلوبة رقميا والقيمة 0 إذا كان عكس ذلك.

إذا كانت قيمة الرجوع هي 1 فسيكون الحل في الجدول b.

خلال كل كرة يتم إظهار المصفوفة Ak والعنصر الثاني bk.

 تساوي الثابتة NMAX البعد القصوي للمصفوفة زائد 1، وتساوي الثابتة N2MAX القيمة NMAX+1

• int sl_gauss_aff(double a[NMAX][NMAX],double b[NMAX],int n)
  {
   int i,j,k,l,err;
   double pivot,coef,s;
   double t[NMAX][N2MAX];
   for(i=1;i<=n;i++)
   {
   for(j=1;j<=n;j++)
   t[i][j]=a[i][j];
   t[i][n+1]=b[i];
   }
   err=1;
   k=1;
   while (err==1 && k<n)
   {
   pivot=fabs(t[k][k]);
   l=k;
   while(pivot==0 && l<n)
   {
   l++;
   pivot=fabs(t[l][k]);
   }
   if(pivot!=0)
   {
   if(l!=k)
   for(j=k;j<=n+1;j++)
   {
   pivot=t[k][j];
   t[k][j]=t[l][j];
   t[l][j]=pivot;
   }
   pivot=t[k][k];
   for(i=k+1;i<=n;i++)
   {
   coef=t[i][k]/pivot;
   for(j=1;j<=n+1;j++)
   t[i][j] -= coef*t[k][j];
   }
   printf(" A(%d) b(%d)\n",k+1,k+1);
   for(i=1;i<=n;i++)
   {
   for(j=1;j<=n;j++)
   printf("%12.6e ",t[i][j]);
   printf("I %12.6e \n",t[i][n+1]);
   }
   }
   else err=0;
   k++;
   }
   if(t[n][n]==0) err=0;
   if(err==1)
   {
   b[n]=t[n][n+1]/t[n][n];
   for(i=n-1;i>=1;i--)
   {
   s=t[i][n+1];
   for(j=i+1;j<=n;j++)
   s-=t[i][j]*b[j];
   b[i]=s/t[i][i];
   }
   }
   return(err);
  }

I'm reading: طريقة غوص

بقلم soufian najim

سفيان، احب أن أضع كل ما أعرف من معلومات حول الحاسوب والتقنيات الجديدة، وخطرت لي فكرة عمل مدونة تضم كل المجالات التعليمية التي أستطيع إفادتكم بها ، فأرجوا ان لاتبخلوا علي أيضا بمتابعتكم لمواضيعي كما ان تعليقاتكم تهمني وتزيد من عطائي لكم إخوتي الكرام وأي استفسار ان موجود وشكرا

قسم : الرئيسية